范某帅的博客
0%

数据结构-第五章-树与二叉树

发表于 更新于 分类于 阅读次数： Valine：
本文字数： 9.1k 阅读时长 ≈ 8 分钟

二叉树的存储

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
#include<stdio.h>
#include <malloc.h>
#define Maxsize 100

//顺序存储
struct TreeNode
{
	int value;
	bool isEmpty;
};

//定义
//TreeNode t[Maxsize];
//for (int i = 0; i < Maxsize; i++)
//{
//	t[i].isEmpty = true;
//}

//二叉树的链式存储
struct ElemType
{
	int value;
};

typedef struct BiTNode {
	ElemType data;
	struct BiTNode* left_child, * right_child, * parent;
}BiTNode, * BiTree;

int main() {
	//定义一颗空树
	BiTree root = NULL;
	//插入空结点
	root = (BiTree)malloc(sizeof(BiTree));
	root->data.value = { 1 };
	root->left_child = NULL;
	root->right_child = NULL;
	root->parent = NULL;
	//插入新的结点
	BiTNode* point = (BiTNode*)malloc(sizeof(BiTNode));
	point->data.value = { 2 };
	point->left_child = NULL;
	point->right_child = NULL;
	point->parent = root;
	root->left_child = point;
	return 0;
}

二叉树的先中后序遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
#include<stdio.h>
#include <malloc.h>

struct ElemType
{
	int value;
};

typedef struct BiTNode {
	ElemType data;
	struct BiTNode* left_child, * right_child;
}BiTNode, * BiTree;

void visit(BiTNode B) {
	printf("%d\n", B.data.value);
}

void visit(BiTree B) {
	printf("%d\n", B->data.value);
}

//先序遍历
void PreOrder(BiTree T) {
	if (T != NULL)
	{
		visit(T);
		PreOrder(T->left_child);
		PreOrder(T->right_child);
	}
}

//中序遍历
void InOrder(BiTree T) {
	if (T != NULL)
	{
		InOrder(T->left_child);
		visit(T);
		InOrder(T->right_child);
	}
}

//后序遍历
void PostOrder(BiTree T) {
	if (T != NULL)
	{
		PostOrder(T->left_child);
		PostOrder(T->right_child);
		visit(T);
	}
}

//求树的深度
int treeDepth(BiTree T) {
	if (T == NULL)
	{
		return 0;
	}
	else
	{
		int left = treeDepth(T->left_child);
		int right = treeDepth(T->right_child);
		return left > right ? left + 1 : right + 1;
	}
}

int main() {
	return 0;
}

二叉树的层次遍历

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
#include<stdio.h>
#include <malloc.h>

//二叉树的链式存储
typedef struct BiTNode {
	char data;
	struct BiTNode* left_child, * right_child;
}BiTNode, * BiTree;

//链式队列结点
typedef struct LinkNode {
	BiTNode* data;
	struct LinkNode* next;
}LinkNode;

//队头队尾
typedef struct {
	LinkNode* front, * rear;
}LinkQueue;

void visit(BiTNode B) {
	printf("%c\n", B.data);
}

void visit(BiTree B) {
	printf("%c\n", B->data);
}

//初始化队列 带头结点
void InitQueue(LinkQueue &Q) {
	Q.front = Q.rear = (LinkNode*)malloc(sizeof(LinkNode));
	Q.front->next = NULL;
}

//是否为空
bool isEmpty(LinkQueue Q) {
	return Q.front == Q.rear;
}

//新元素入队
void EnQueue(LinkQueue &Q, BiTNode* element) {
	LinkNode* new_point = (LinkNode*)malloc(sizeof(LinkNode));
	new_point->data = (BiTNode*)malloc(sizeof(BiTNode));
	new_point->data = element;
	new_point->next = NULL;
	Q.rear->next = new_point;
	Q.rear = new_point;
}

//出队
void DeQueue(LinkQueue &Q, BiTree& T) {
	if (Q.front == Q.rear)
	{
		printf("队列为空");
	}
	else
	{
		LinkNode* new_point = Q.front->next;
		T = new_point->data;
		Q.front->next = new_point->next;
		if (Q.rear == new_point)
		{
			Q.rear = Q.front;
		}
		free(new_point);
	}
}

//根据先序排列建立二叉树
BiTNode* InitTree() {
	BiTNode* point = NULL;
	char ch;
	scanf_s("%c", &ch);
	if (ch == '#')
	{
		point == NULL;
	}
	else
	{
		point = (BiTNode*)malloc(sizeof(BiTNode));
		point->data = ch;
		point->left_child = InitTree();
		point->right_child = InitTree();
	}
	return point;
}

//层序遍历
void LevelOrder(BiTree T) {
	LinkQueue Q;
	InitQueue(Q);
	BiTree point;
	EnQueue(Q, T);
	while (!isEmpty(Q))
	{
		DeQueue(Q, point);
		visit(point);
		if (point->left_child)
		{
			EnQueue(Q, point->left_child);
		}
		if (point->right_child)
		{
			EnQueue(Q, point->right_child);
		}
	}
}

int main() {
	BiTree T = InitTree();
	LevelOrder(T);
	return 0;
}

二叉树的线索化

1
2
3
4
5
typedef struct ThreadNode {
	int data;
	struct ThreadNode* left_child, * right_child;
	int left_flag, right_flag;
}ThreadNode, * ThreadTree;

中序线索化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include<stdio.h>

typedef struct ThreadNode {
	char data;
	struct ThreadNode* left_child, * right_child;
	int left_flag, right_flag;
}ThreadNode, * ThreadTree;

//全局变量pre，指向当前访问结点的前驱
ThreadNode* pre = NULL;

void visit(ThreadNode *point) {
	if (point->left_child == NULL)
	{
		point->left_child = pre;
		point->left_flag = 1;
	}
	if (pre != NULL && pre->right_child == NULL)
	{
		pre->right_child = point;
		pre->right_flag = 1;
	}
	pre = point;
}

//中序遍历二叉树，一边遍历一边线索化
void InThread(ThreadTree T) {
	if (T != NULL)
	{
		InThread(T->left_child);
		visit(T);
		InThread(T->right_child);
	}
}

//中序线索化二叉树
void CreateInThread(ThreadTree T) {
	if (T != NULL)
	{
		InThread(T);
		if (pre->right_child == NULL)
		{
			pre->right_flag = 1;
		}
	}
}

先序线索化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
#include<stdio.h>

typedef struct ThreadNode {
	char data;
	struct ThreadNode* left_child, * right_child;
	int left_flag, right_flag;
}ThreadNode, * ThreadTree;

//全局变量pre，指向当前访问结点的前驱
ThreadNode* pre = NULL;

void visit(ThreadNode *point) {
	if (point->left_child == NULL)//左子树为空，建立前驱线索
	{
		point->left_child = pre;
		point->left_flag = 1;
	}
	if (pre != NULL && pre->right_child == NULL)
	{
		pre->right_child = point;//建立前驱节点的后继线索
		pre->right_flag = 1;
	}
	pre = point;
}

//先序遍历二叉树，一边遍历一边线索化
void PreThread(ThreadTree T) {
	if (T != NULL)
	{
		visit(T);
		if (T->left_flag == 0)
		{
			PreThread(T->left_child);
		}
		PreThread(T->right_child);
	}
}

//先序线索化二叉树
void CreatePreThread(ThreadTree T) {
	if (T != NULL)
	{
		PreThread(T);
		if (pre->right_child == NULL)
		{
			pre->right_flag = 1;//处理遍历的最后一个节点
		}
	}
}

后序线索化

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
#include<stdio.h>

typedef struct ThreadNode {
	char data;
	struct ThreadNode* left_child, * right_child;
	int left_flag, right_flag;
}ThreadNode, * ThreadTree;

//全局变量pre，指向当前访问结点的前驱
ThreadNode* pre = NULL;

void visit(ThreadNode *point) {
	if (point->left_child == NULL)//左子树为空，建立前驱线索
	{
		point->left_child = pre;
		point->left_flag = 1;
	}
	if (pre != NULL && pre->right_child == NULL)
	{
		pre->right_child = point;//建立前驱节点的后继线索
		pre->right_flag = 1;
	}
	pre = point;
}

//后序遍历二叉树，一边遍历一边线索化
void PostThread(ThreadTree T) {
	if (T != NULL)
	{
		PostThread(T->left_child);
		PostThread(T->right_child);
		visit(T);
	}
}

//后序线索化二叉树
void CreatePreThread(ThreadTree T) {
	if (T != NULL)
	{
		PostThread(T);
		if (pre->right_child == NULL)
		{
			pre->right_flag = 1;//处理遍历的最后一个节点
		}
	}
}

线索二叉数中照前驱后继

树的顺序存储（双亲表示法）

1
2
3
4
5
6
7
8
9
10
11
12
#include<stdio.h>
#define Max_Tree_Size 100

typedef struct {
	char data;
	int parent;
}PTNode;

typedef struct {
	PTNode nodes[Max_Tree_Size];
	int num;
}PTreee;

删除元素（方案二） 将最后一个元素替换到要删除元素的位置

缺点 查找指定元素的时候只能从头开始遍历

树的顺序+链式存储（孩子表示法）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
#include<stdio.h>
#define Max_Tree_Size 100

struct CTNode
{
	int child;//孩子结点在数组中的位置
	struct CTNode* next;//下一个孩子
};

typedef struct {
	int data;
	struct CTNode* firstChild;//指向第一个孩子
}CTBox;

typedef struct {
	CTBox nodes[Max_Tree_Size];
	int num, root;//结点数和根的位置
}CTree;

树的链式存储（孩子兄弟表示法）

1
2
3
4
5
6
#include<stdio.h>

typedef struct CSNode {
	int data;
	struct CSNode* first_child, * next_sibling;//第一个孩子 和 右兄弟指针
};

树和森林的遍历

二叉排序树的定义

二叉排序树的构建和查找

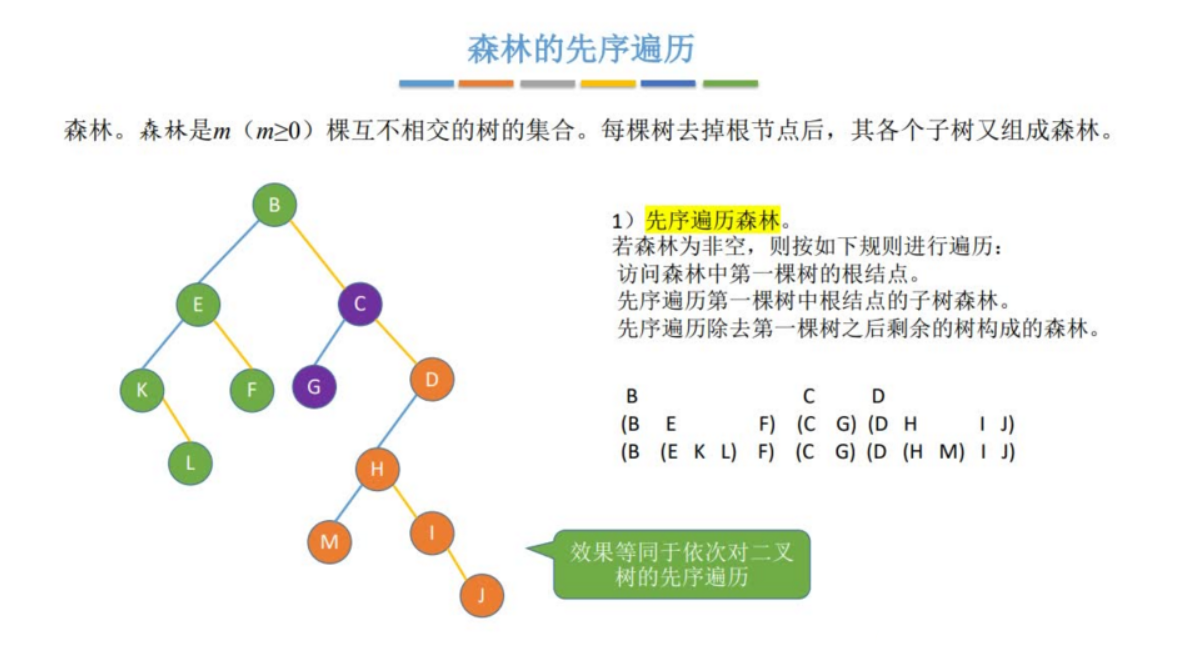
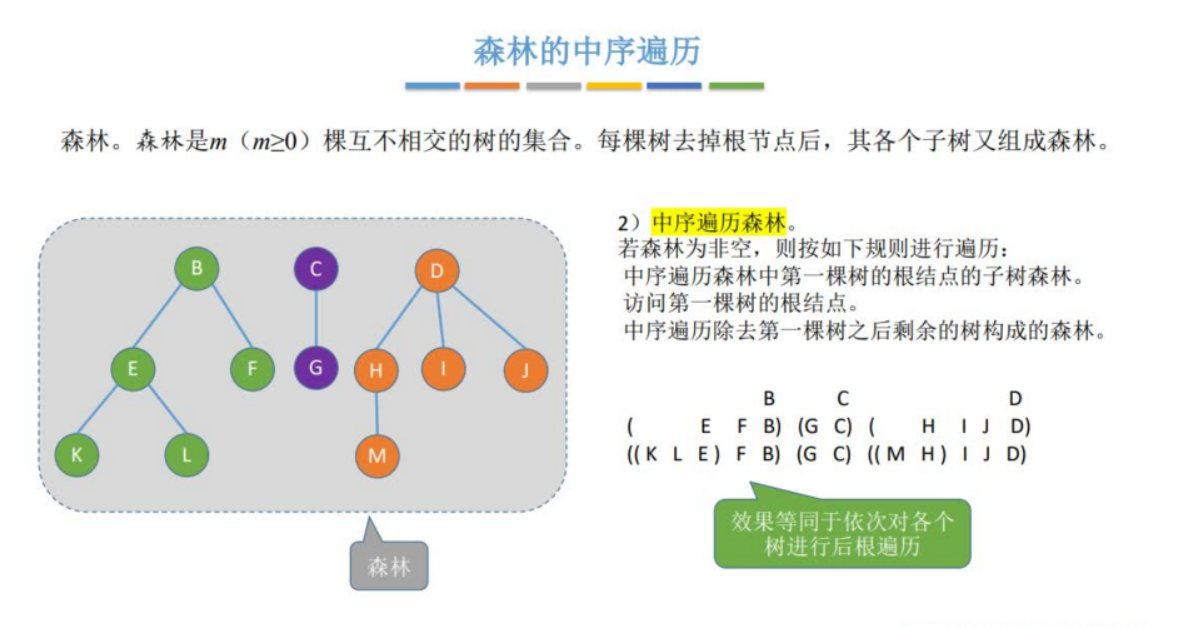
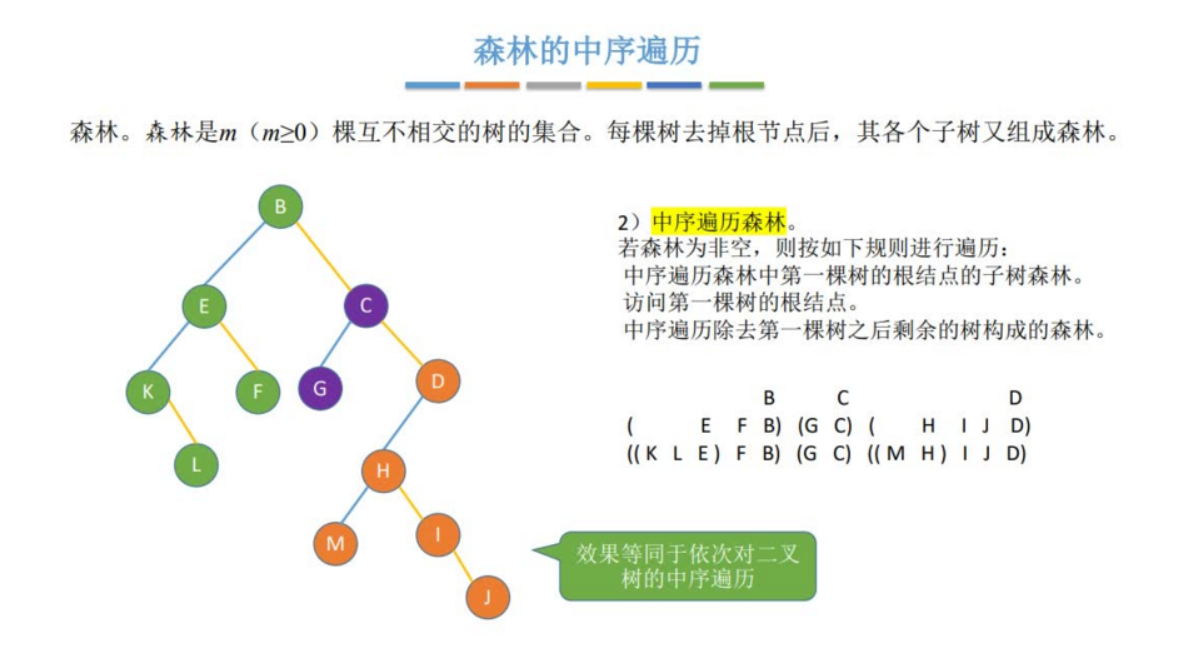
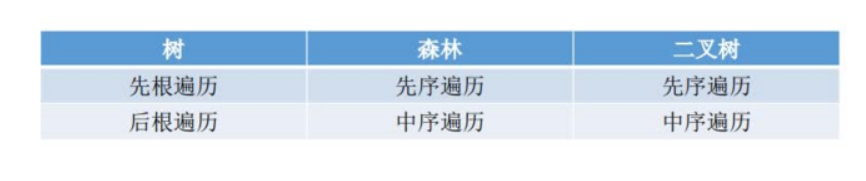
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
#include<stdio.h>
#include <malloc.h>

//二叉排序树的结点
typedef struct BSTNode {
	int key;
	struct BSTNode* left_child, * right_child;
}BSTNode, * BSTree;

//在二叉排序树中查找值为key的结点 最坏空间复杂度 O(1)
BSTNode* BST_Search(BSTree T, int key) {
	while (T != NULL && key != T->key)
	{
		if (key < T->key)//小于在左子树上查找
		{
			T = T->left_child;
		}
		else//大于在右子树上查找
		{
			T = T->right_child;
		}
	}
	return T;
}

//递归实现二叉排序树的查找 最坏空间复杂度 O(h)
BSTNode* BSTSearch(BSTree T, int key) {
	if (T == NULL)
	{
		return NULL;
	}
	if (key == T->key)
	{
		return T;
	}
	else if (key < T->key)
	{
		BSTSearch(T->left_child, key);
	}
	else
	{
		BSTSearch(T->right_child, key);
	}
}

//二叉排序树的插入
void BST_Insert(BSTree &T, int value) {
	if (T == NULL)
	{
		T = (BSTree)malloc(sizeof(BSTNode));
		T->key = value;
		T->left_child = T->right_child = NULL;
		printf("插入数据%d成功\n", value);
	}
	else if (value == T->key)
	{
		printf("存在相同的数据，插入失败！");
	}
	else if (value < T->key)
	{
		BST_Insert(T->left_child, value);
	}
	else
	{
		BST_Insert(T->right_child, value);
	}
}

//根据关键字数组构建二叉排序树
void Create_BST(BSTree &T, int value[], int num) {
	T = NULL;
	int i = 0;
	while (i < num)
	{
		BST_Insert(T, value[i]);
		i += 1;
	}
}

int main() {
	BSTree T;
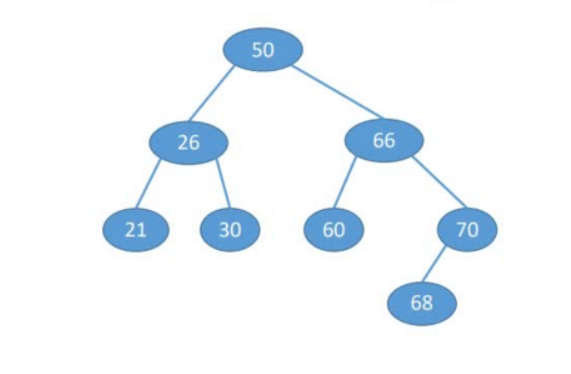
	int data[] = { 50,66,60,26,21,30,70,68 };
	Create_BST(T, data, (sizeof(data)/sizeof(data[0])));
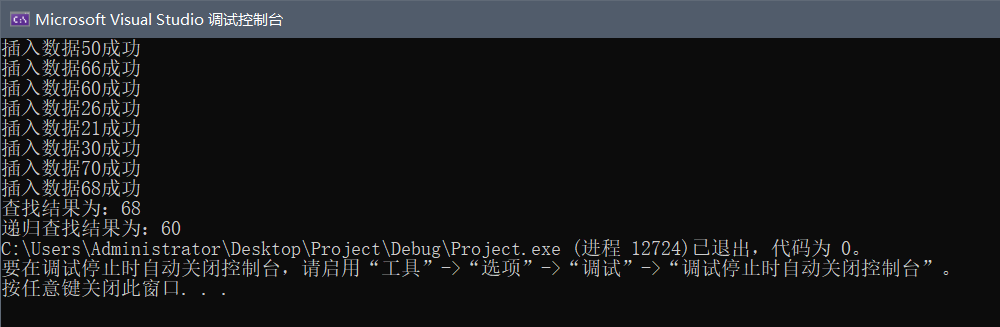
	BSTNode* result = BST_Search(T, 68);
	printf("查找结果为：%d", result->key);
	BSTNode* res = BSTSearch(T, 60);
	printf("\n递归查找结果为：%d", res->key);
	return 0;
}

平衡二叉树

二叉树插入和调整最小不平衡子树是重点

查找效率分析看看这个图个乐

哈夫曼树

本文标题:数据结构-第五章-树与二叉树

文章作者:fanchen

发布时间:2021年06月05日 - 09:58:15

最后更新:2021年06月06日 - 18:54:43

原始链接:http://88fanchen.github.io/posts/abac19d0/

许可协议:署名-非商业性使用-禁止演绎 4.0 国际 转载请保留原文链接及作者。